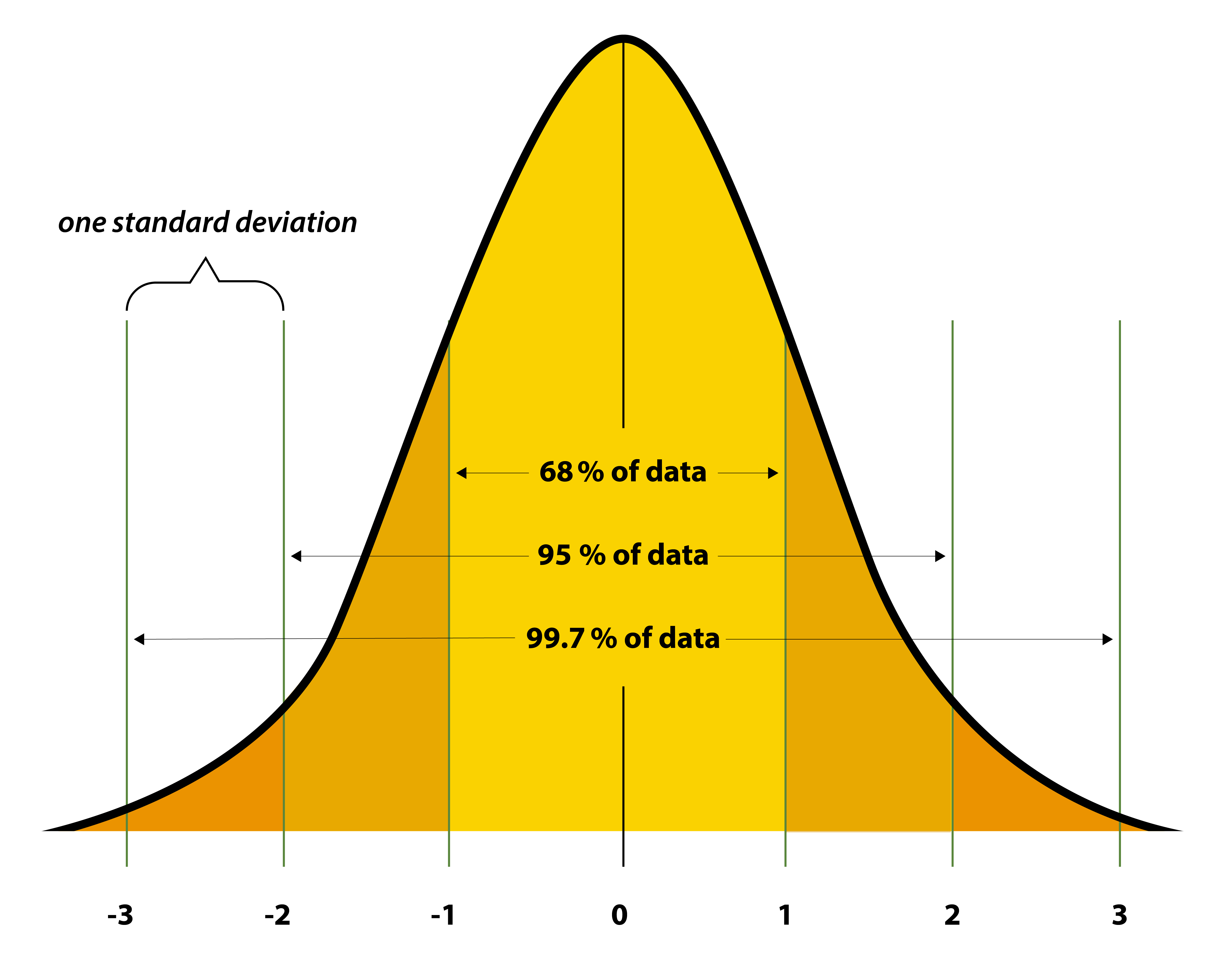
A distribution or histogram is a representation of the results we see in given situations. Distributions can be used to portray data used in everyday life, such as test scores, salaries, and even blood pressure. When the distribution is normal, the histogram takes on a bell shape, which is why it is sometimes referred to as a “bell curve.” A standard normal distribution, also called the z-distribution, is the most commonly used normal distribution with a mean of 0 and a standard deviation of 1. In the standard normal distribution, 68% of data falls within 1 standard deviation of the mean, 95% falls within 2 standard deviations, and 99.7% falls within 3 standard deviations of the mean. Consider the image of the bell curve.¹

In all normal distributions, the area under the curve is 1, the curve is symmetrical around the mean, and exactly half of the data falls on the right and left of the mean.

An example of a bell curve distribution would be if students in a math class took a final exam, and the class score average was 75% and the standard deviation was 5 percentage points. If the class scores follow a normal distribution, then this means that:

• 68% of the students received a score between 70% and 80% on the exam, or the mean (75%) plus or minus 1 standard deviation (5).
• 95% of students received a score between 65% and 85% on the exam, or the mean (75%) plus or minus 2 standard deviations (10).
• 99.7% of students received a score between 60% and 90% on the exam, or the mean (75%) plus or minus 3 standard deviations (15).

1. "Image 6: Standard normal distribution curve." Sampling Distributions for Counts and Proportions. University of North Carolina, Freeman and Company. 2009.