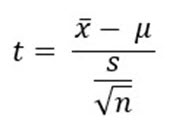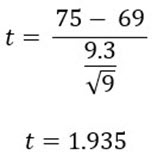A t-test is used to determine if there is a significant difference between the means of two groups. To compare the average height of students in the class to the average height of students in the entire school, a t-test is required. A t-test is used when the population standard deviation is unknown and data points are normally distributed.

The first step of the test is to state the null and alternative hypotheses. Again, these are the statements that we will be comparing to each other to determine which one is correct. This test ultimately seeks to determine if there is any statistically significant difference between the average height of the class and the school, not necessarily greater or lower.

The formula for the t-test is as follows:

In this equation, x̄ is the sample mean, μ is the population mean, s is the sample standard deviation, and n is the number of observations in the sample. The sample mean (75), the sample standard deviation (9.3), and the number of observations in the sample (9) are all known. Assume the average height of students in the school is 69 inches: